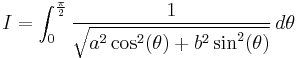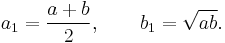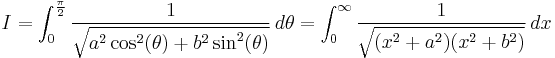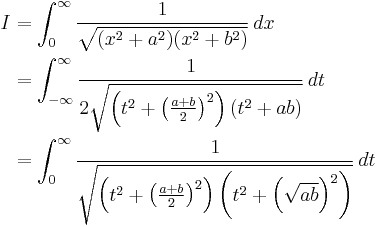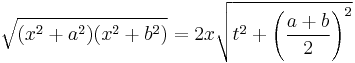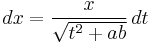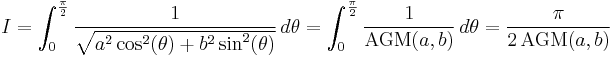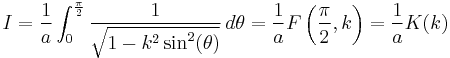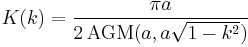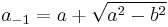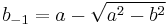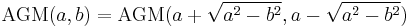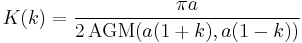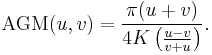Landen's transformation

Landen's transformation, independently rediscovered by Gauss, is a mapping of the parameters of an elliptic integral, which leaves the value of the integral unchanged.

In Gauss's formulation,

I = \int _0^{\frac{\pi}{2}}\frac{1}{\sqrt{a^2 \cos^2(\theta) %2B b^2 \sin^2(\theta)}} \, d \theta

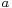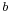is unchanged if \scriptstyle{a} and \scriptstyle{b} are replaced by their arithmetic and geometric means respectively, that is

a_1 = \frac{a %2B b}{2},\qquad b_1 = \sqrt{a b}.\,

Proof

The transformation, may be achieved purely by integration by substitution. It is convenient to first cast the integral in an algebraic form by a substitution of 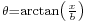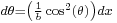\scriptstyle{\theta = \arctan\left( \frac{x}{b}\right)}, \scriptstyle{d \theta = \left( \frac{1}{b}\cos^{2}(\theta)\right) d x} giving

I = \int _0^{\frac{\pi}{2}}\frac{1}{\sqrt{a^2 \cos^2(\theta) %2B b^2 \sin^2(\theta)}} \, d \theta = \int _0^\infty \frac{1}{\sqrt{(x^2 %2B a^2) (x^2 %2B b^2)}} \, dx

A further substitution of 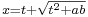\scriptstyle{x = t %2B \sqrt{t^{2} %2B a b}} gives the desired result (in the algebraic form)

\begin{align}I & = \int _0^\infty \frac{1}{\sqrt{(x^2 %2B a^2) (x^2 %2B b^2)}} \, dx \\ & = \int _{- \infty}^\infty \frac{1}{2 \sqrt{\left( t^2 %2B \left( \frac{a %2B b}{2}\right)^2 \right) (t^2 %2B a b)}} \, dt \\ & = \int _0^\infty\frac{1}{\sqrt{\left( t^2 %2B \left( \frac{a %2B b}{2}\right)^2\right) \left(t^2 %2B \left(\sqrt{a b}\right)^2\right)}} \, dt \end{align}

This latter step is facilitated by writing the radical as

\sqrt{(x^2 %2B a^2) (x^2 %2B b^2)} = 2x \sqrt{t^2 %2B \left( \frac{a %2B b}{2}\right)^2}

and the infinitesimal as

dx = \frac{x}{\sqrt{t^2 %2B a b}} \, dt

so that the factor of 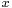\scriptstyle{x} is easily recognized and cancelled between the two factors.

Arithmetic-geometric mean and Legendre's first integral

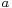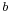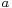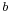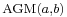If the transformation is iterated a number of times, then the parameters \scriptstyle{a} and \scriptstyle{b} converge very rapidly to a common value, even if they are initially of different orders of magnitude. The limiting value is called the arithmetic-geometric mean of \scriptstyle{a} and \scriptstyle{b}, \scriptstyle{\operatorname{AGM}(a,b)}. In the limit, the integrand becomes a constant, so that integration is trivial

I = \int _0^{\frac{\pi}{2}} \frac{1}{\sqrt{a^2 \cos^2(\theta) %2B b^2 \sin^2(\theta)}} \, d\theta = \int _0^{\frac{\pi}{2}}\frac{1}{\operatorname{AGM}(a,b)} \, d\theta = \frac{\pi}{2 \,\operatorname{AGM}(a,b)}

The integral may also be recognized as a multiple of Legendre's complete elliptic integral of the first kind. Putting 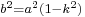\scriptstyle{b^2 = a^2 (1 - k^2)}

I = \frac{1}{a} \int _0^{\frac{\pi}{2}} \frac{1}{\sqrt{1 - k^2 \sin^2(\theta)}} \, d\theta = \frac{1}{a} F\left( \frac{\pi}{2},k\right) = \frac{1}{a} K(k)

Hence, for any 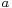\scriptstyle{a}, the arithmetic-geometric mean and the complete elliptic integral of the first kind are related by

K(k) = \frac{\pi a}{2 \, \operatorname{AGM}(a,a \sqrt{1 - k^2})}

By performing an inverse transformation (reverse arithmetic-geometric mean iteration), that is

a_{-1} = a %2B \sqrt{a^2 - b^2} \,
b_{-1} = a - \sqrt{a^2 - b^2} \,
\operatorname{AGM}(a,b) = \operatorname{AGM}(a %2B \sqrt{a^2 - b^2},a - \sqrt{a^2 - b^2}) \,

the relationship may be written as

K(k) = \frac{\pi a}{2 \, \operatorname{AGM}(a (1 %2B k),a (1 - k))} \,

which may be solved for the AGM of a pair of arbitrary arguments;

\operatorname{AGM}(u,v) = \frac{\pi (u %2B v)}{4 K\left( \frac{u - v}{v %2B u}\right)}.
The definition adopted here for 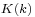\scriptstyle{K(k)}, differs from that used in the arithmetic-geometric mean article, such that 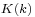\scriptstyle{K(k)} here is 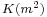\scriptstyle{K(m^{2})} in that article.

References